Arquímedes de Siracusa fue un físico, ingeniero, inventor,astrónomo y matemático griego. Es considerado uno de los científicos más importantes de la antigüedad clásica. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes, que lleva su nombre.
Se considera que Arquímedes fue uno de los matemáticos más grandes de la antigüedad y, en general, de toda la historia. Usó el método exhaustivo para calcular el área bajo el arco de una parábola con el sumatorio de una serie infinita, y dio una aproximación extremadamente precisa del número PI. También definió la espiral que lleva su nombre, fórmulas para los volúmenes de las superficies de revolución y un ingenioso sistema para expresar números muy largos.
Si bien la faceta de inventor de Arquímedes es quizás la más popular, también realizó importantes contribuciones al campo de las matemáticas.
Arquímedes fue capaz de utilizar los infinitesimales de forma similar al modernocálculo integral. A través de la reducción al absurdo (reductio ad absurdum), era capaz de contestar problemas mediante aproximaciones con determinado grado de precisión, especificando los límites entre los cuales se encontraba la respuesta correcta. Esta técnica recibe el nombre de método exhaustivo, y fue el sistema que utilizó para aproximar el valor del número π. Para ello, dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos. A medida que se incrementa el número de lados del polígono la diferencia se acorta, y se obtiene una aproximación más exacta.
En su obra sobre La cuadratura de la Parábola, Arquímedes probó que el área definida por una parábola y una línea recta equivalía exactamente a 4/3 el área del correspondiente triángulo inscrito, tal y como se puede observar en la figura de la derecha. Para obtener ese resultado, desarrolló una serie geométrica infinita con una razón común de 1/4:
El primer término de esta suma equivale al área del triángulo, el segundo sería la suma de las áreas de los dos triángulos inscritos en las dos áreas delimitadas por el triángulo y la parábola, y así sucesivamente. Esta prueba utiliza una variación de la serie infinita 1/4 + 1/16 + 1/64 + 1/256 + ..., cuya suma se demuestra que equivale a1/3.
referencia:
http://es.wikipedia.org/wiki/Arqu%C3%ADmedes


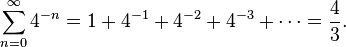
No hay comentarios:
Publicar un comentario